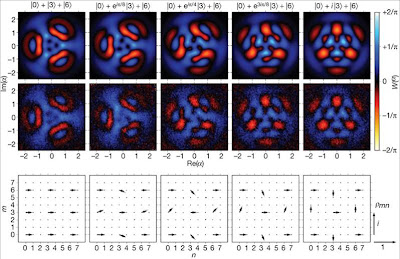
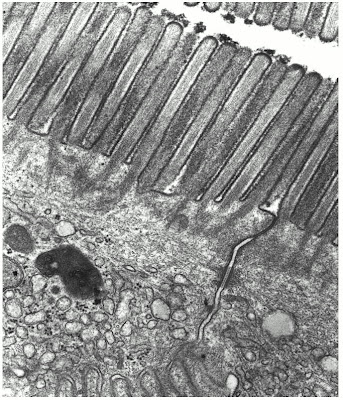
Emergence versus reductionism
In the final chapter of his book, A Different Universe , Bob Laughlin states: while a simple and absolute law, such as hydrodynamics, can evolve from the deeper laws underneath, it is at the same time independent of them, in that it would be the same even if the deeper laws were changed. Thinking through these effects seriously moves one to ask which law is the more ultimate , the details from which everything flows or the transcendent, emergent law they generate. That question is semantic and thus has no absolute answer, but it is clearly a primitive version of the moral conundrum raised by the alleged subordination of the laws of living to the laws of chemistry and physics. It shows allergorically how a person could easily master one and learn nothing whatsoever about the other. The epistemological barrier is not mystical but physical. The conflict between these two conceptions of the ultimate : the laws of the parts or the laws of the collective is very ancient and not reso