There is a nice paper
Strong-versus weak-coupling paradigms for cuprate superconductivity
S Asban, M Shay, M Naamneh, T Kirzhner, A Keren
They report very careful measurements of the resistivity versus temperature for four different classes of cuprate superconductors at optimal doping. The goal is to test Homes relation which relates the normal state resistivity to the superfluid density.
Aside: surely it is not appropriate to call this Homes law. Somehow, it does not have the status of Newton's laws or thermodynamics...
In particular, they compare their results to two distinctly different theoretical models that claim to explain Homes relation.
The first model is a conventional "weak-coupling" BCS model for the superconductivity with the resistivity dominated by disorder. One problem with applying this model is that it does not capture the large temperature dependence of the resistivity and that the YBCO materials appear to be particularly clean.
The second model is a hard core boson model, assuming that Cooper pairs still exist well above the superconducting transition temperature. This "strong coupling model" is due to Lindner and Auerbach. In addition to describing Homes relation it also gives a large resistivity, that is linear in temperature, and comparable to the Mott-Ioffe-Regel limit, characteristic of bad metals. One potential problem with this model is that it is only directly relevant to optimally doped curates, whereas the Homes relations seems to hold more or less independently of doping. A major prediction of the model is the relation below, which does not really have any free parameters,
Lambda is the London penetration depth; its inverse square is related to the superfluid density.
The figure below summarises the main results of the paper. The line with q=2 corresponds to the predictions of the above equation.
It is really a matter of personal taste as to whether the above results represent "good" agreement between experiment and theory. As noted in the paper, accurately determining the penetration depth is a tricky business.
The authors also find that, except for YBCO, the resistivity is never really strictly linear in temperature, but only approximately so. This is important because many theorists, particularly the AdS-CFT crowd, assume it is and place great stock on producing a theory with a linear in T resistivity.
There are a couple of things that I like about this paper, compared to your average experimental paper.
First, the authors seem to have been incredibly careful about their measurements. They use different film samples with different thicknesses and different distances between contacts. They check for ohmic behaviour. They see how the resistance varies with "identical" bridges.
Second, the authors compare their results to more than one theory, the goal being to hopefully rule out one of them. This is in the spirit of the method of multiple alternative hypotheses.
I thank Assa Auerbach bringing this paper to my attention. He comments on it via my earlier post on his work on the hard-core boson model.
Friday, January 31, 2014
Wednesday, January 29, 2014
A basic but important research skill, 2: checking results
Earlier I posted about a basic skill: take initiative! Don't wait for someone else to tell you what to do. Try stuff.
It is exciting when you think that you have finally obtained some research results. It is even more exciting if they seem interesting and potentially important. But, don't fool yourself. They may be wrong! Mistakes happen in research. More often than many want to admit. Furthermore, the more complicated the technique and the system under investigation, the more likely something will go wrong. Murphy's law!
So how do you check your results? I am not sure. There is no simple universal procedure to check results. Just repeating the experiment or calculation is not good enough. You [or the instrument or software...] may be making the same mistake.
Learning to check results is an art and requires patience, discipline, and creativity.
Furthermore, different individuals and different research fields often have quite different standards as to how many different checks one should perform. Some seem to rush to publish once they get an "interesting" result. Others, are very cautious and careful and perform multiple checks.
I am very thankful that many of my collaborators over the years have been more conscientious than me.
For students: here are a few ideas as to some basic checks that one should do.
Compare your results to relevant published work. Make sure you can reproduce earlier work. If not, do you have a good reason to believe you are right and they are wrong.
Computational work.
Compare your results to limits [e.g. weak or strong coupling, for which one can obtain analytical results].
Use different versions of software or numerical methods.
For short programs, write two codes from scratch.
Analytical calculations.
Compare your results to Mathematica or a numerical calculation.
Experiments.
Change the sample, device, material, instrument, or procedure.
Computational chemistry.
Try different basis sets and levels of theory. Don't just do DFT! When possible, benchmark it against smaller systems.
Curve fitting.
Have different individuals do it independently and see if they get the same result.
What do you think are good procedures for checking results?
When should you quit checking?
It is exciting when you think that you have finally obtained some research results. It is even more exciting if they seem interesting and potentially important. But, don't fool yourself. They may be wrong! Mistakes happen in research. More often than many want to admit. Furthermore, the more complicated the technique and the system under investigation, the more likely something will go wrong. Murphy's law!
So how do you check your results? I am not sure. There is no simple universal procedure to check results. Just repeating the experiment or calculation is not good enough. You [or the instrument or software...] may be making the same mistake.
Learning to check results is an art and requires patience, discipline, and creativity.
Furthermore, different individuals and different research fields often have quite different standards as to how many different checks one should perform. Some seem to rush to publish once they get an "interesting" result. Others, are very cautious and careful and perform multiple checks.
I am very thankful that many of my collaborators over the years have been more conscientious than me.
For students: here are a few ideas as to some basic checks that one should do.
Compare your results to relevant published work. Make sure you can reproduce earlier work. If not, do you have a good reason to believe you are right and they are wrong.
Computational work.
Compare your results to limits [e.g. weak or strong coupling, for which one can obtain analytical results].
Use different versions of software or numerical methods.
For short programs, write two codes from scratch.
Analytical calculations.
Compare your results to Mathematica or a numerical calculation.
Experiments.
Change the sample, device, material, instrument, or procedure.
Computational chemistry.
Try different basis sets and levels of theory. Don't just do DFT! When possible, benchmark it against smaller systems.
Curve fitting.
Have different individuals do it independently and see if they get the same result.
What do you think are good procedures for checking results?
When should you quit checking?
Labels:
basics,
better science,
curve fitting,
job advice
Tuesday, January 28, 2014
Concerted vs sequential processes in chemistry
A basic but important and interesting question in physical chemistry concerns a chemical reaction or process that involves two steps: A to B to C.
Do they occur sequentially or can they occur simultaneously, i.e., in a concerted or co-operative manner?
Two examples of particular interest are coupled electron-proton transfer and double proton transfer.
The figure below shows a carboxylic acid dimer involving two hydrogen bonds
Do they occur sequentially or can they occur simultaneously, i.e., in a concerted or co-operative manner?
Two examples of particular interest are coupled electron-proton transfer and double proton transfer.
The figure below shows a carboxylic acid dimer involving two hydrogen bonds
The configuration above has the same energy as the tautomer with the top H moved to the right and the bottom H moved to the left. But, does this reaction occur by simultaneously moving the protons or first moving one and then the second.
For the case of double proton transfer in dimers of a model of a DNA base pair [shown in the picture below] there has been some controversy about whether the process is concerted or sequential. This brief letter by Kwon and Zewail in PNAS gives the relevant references. They stress that some of the controversy seems to stem from confusion about clearly defining what one means by the two options. They argue the weight of the evidence is for sequential.
Another example concerns the role of intermediate electronic states in charge separation processes in molecular photovoltaic materials.
I am interested in exploring simple effective Hamiltonians that might be used to come up with some general criteria and experimental signatures for discriminating between concerted and sequential processes.
Thursday, January 23, 2014
To the barricades!
Last year the article, The neoliberal assault on academia by Tarak Barkawi, was brought to my attention. It was originally published as an Opinion piece in Aljazeera and has generated some interest and discussion.
First, what is "neoliberalism"? According to Wikipedia
Yet I am reluctant to admit that there are a couple of ideas in the article that are painfully true.
A. The changes that are happening in universities reflect changes in broader society.
B. New administrative procedures such the Research Assessment Exercise in the UK, uniform course profiles, widespread use of metrics for staff assessment, are not just annoying bureaucratic exercises. They reflect a deep underlying and unquestioned ideology and a desire to control. One who warned about this trend in society was the French scholar Jacques Ellul:
First, what is "neoliberalism"? According to Wikipedia
The term "neoliberal" is now used mainly by those who are critical of legislative initiatives that push for free trade, deregulation, enhanced privatization, and an overall reduction in government control of the economy.The article is written with a quasi-Marxist tone, emphasising class struggle. This may put off some.
Yet I am reluctant to admit that there are a couple of ideas in the article that are painfully true.
A. The changes that are happening in universities reflect changes in broader society.
B. New administrative procedures such the Research Assessment Exercise in the UK, uniform course profiles, widespread use of metrics for staff assessment, are not just annoying bureaucratic exercises. They reflect a deep underlying and unquestioned ideology and a desire to control. One who warned about this trend in society was the French scholar Jacques Ellul:
"the totality of methods rationally arrived at and having absolute efficiency (for a given stage of development) in every field of human activity."[18]
The following acid observation by Barkawi is particularly hitting:
Here is the intersection with neoliberal management culture. Neoliberal managers thrive not by bringing in new resources - since austerity is always the order of the day - but by constantly rearranging the deck chairs. Each manager seeks to reorganise and restructure in order to leave his or her mark. They depart for the next lucrative job before the ship goes under.
Labels:
funding,
metrics,
neoliberalism,
politics,
teaching
Wednesday, January 22, 2014
Seeking definitive signatures of quantum criticality
Generally I am skeptical about quantum criticality as an important organising principle for strongly correlated electron materials (see for example, this earlier post, Are elemental metals quantum critical?). The most significant evidence is probably in heavy fermion compounds. However, particularly in the cuprates, I see quantum criticality as one of several competing "hand waiving" explainations of unusual properties. It is important to keep coming back to the idea that a true quantum critical point (QCP) will be associated with some diverging correlation length for some type of "order". Furthermore, this should lead to power laws in physical quantities over several orders in magnitude.
There is an interesting paper
Transport near a quantum critical point in BaFe2(As1−xPx)2
James G. Analytis, H-H. Kuo, Ross D. McDonald, Mark Wartenbe, P. M. C. Rourke, N. E. Hussey, and I. R. Fisher
The relevant background and context is this review article which contains the figure below
A few comments on the paper.
1. At room temperature the resistivity becomes of the order of the Mott-Ioffe-Regel limit, characteristic of a bad metal.
2. The low temperatures the metal is always a Fermi liquid [at least has a resistivity with a quadratic temperature dependence] even at dopings very close to the putative QCP. This is seen in the next figure.
3. The graph below shows the temperature dependence of the slope of the resistivity. It is striking that at high temperatures it has the approximately the same value, independent of doping. This is consistent with an earlier claim of such universality, [that even extended to elemental metals!]
4. The data above only shows a linear in T resistivity [which is often associated with quantum criticality], over less than one decade of temperature.
5. The figure below shows the doping dependence of the A coefficient of the Fermi liquid resistivity and the effective mass. Note the range of values of A is at most one order of magnitude. The effective mass only changes by about a factor of three.
In quantum critical theory both should diverge at the critical point [dashed line]. However, in the actual experimental data A does not diverge but decreases for the smallest x=0.31. This can be seen with the naked eye in the data above.
7. What about alternative theories?
One candidate must be Selective Mottness, as described in this preprint.
It does predict a significant enhancement doping dependence of the effective mass and the Fermi liquid coherence temperature. I am not sure how the P doping translates to band filling. Hopefully the proponents can comment.
Unlike quantum criticality Selective Mottness is actually based on calculations from a microscopic model with realistic interactions.
There is an interesting paper
Transport near a quantum critical point in BaFe2(As1−xPx)2
James G. Analytis, H-H. Kuo, Ross D. McDonald, Mark Wartenbe, P. M. C. Rourke, N. E. Hussey, and I. R. Fisher
The relevant background and context is this review article which contains the figure below
A few comments on the paper.
1. At room temperature the resistivity becomes of the order of the Mott-Ioffe-Regel limit, characteristic of a bad metal.
2. The low temperatures the metal is always a Fermi liquid [at least has a resistivity with a quadratic temperature dependence] even at dopings very close to the putative QCP. This is seen in the next figure.
3. The graph below shows the temperature dependence of the slope of the resistivity. It is striking that at high temperatures it has the approximately the same value, independent of doping. This is consistent with an earlier claim of such universality, [that even extended to elemental metals!]
4. The data above only shows a linear in T resistivity [which is often associated with quantum criticality], over less than one decade of temperature.
5. The figure below shows the doping dependence of the A coefficient of the Fermi liquid resistivity and the effective mass. Note the range of values of A is at most one order of magnitude. The effective mass only changes by about a factor of three.
In quantum critical theory both should diverge at the critical point [dashed line]. However, in the actual experimental data A does not diverge but decreases for the smallest x=0.31. This can be seen with the naked eye in the data above.
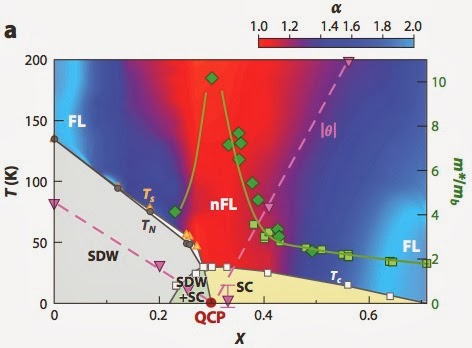
6. The colour shaded plot below shows the exponent n of the resistivity temperature dependence. The dashed line shows the Fermi liquid temperature going to zero at the putative QCP. However, as noted above even at the critical doping a Fermi liquid is always seen at low temperatures.
7. What about alternative theories?
One candidate must be Selective Mottness, as described in this preprint.
It does predict a significant enhancement doping dependence of the effective mass and the Fermi liquid coherence temperature. I am not sure how the P doping translates to band filling. Hopefully the proponents can comment.
Unlike quantum criticality Selective Mottness is actually based on calculations from a microscopic model with realistic interactions.
Monday, January 20, 2014
Significant role of quantum nuclear motion in hydrogen bonding
I recently finished a preprint that I am particularly proud of
Effect of quantum nuclear motion on hydrogen bonding
Ross H. McKenzie, Christiaan Bekker, Bijyalaxmi Athokpam, Sai G. Ramesh
I welcome any comments. I hope to submit to J. Chem. Phys. at the end of the week.
Many of the issues involved I have blogged about before. Here I will just mention two issues that I found particularly interesting. Both relate to the significance of very small changes in bond lengths due to quantum nuclear effects [tunneling and zero-point motion].
In hydrogen bonded complexes [A-H...B] one observes a subtle secondary isotope effect: when the hydrogen atom is replaced by a deuterium atom the distance R between the A and B atoms changes slightly, on the scale of one-hundredth of an Angstrom [and denoted Delta R]. Furthermore, as shown below, the variation of Delta R with R is a non-trivial non-monotonic function.
In the paper we show that for R less than 2.7 A these trends are captured semi-quantitatively by a very simple calculation which assumes that the effect is dominated by the variation with R of the zero-point energy of the A-H stretch.
This leads to the second result that I found both surprising and impressive. When R ~ 2.5 A, the D for H isotope substitution increases R to about 2.54 A. This apparently small change has another secondary effect: it produces a significant change in the energy barrier in the potential energy curve for the A-D stretch, compared to the A-H stretch. This in turn significantly changes the A-D stretch vibrational frequency. Indeed the A-H and A-D stretch can have similar frequencies, whereas for isolated molecules the frequency ratio would be close to 1.4=sqrt(2). This explains rather complicated and large isotope effects I blogged about more than two years ago.
Effect of quantum nuclear motion on hydrogen bonding
Ross H. McKenzie, Christiaan Bekker, Bijyalaxmi Athokpam, Sai G. Ramesh
I welcome any comments. I hope to submit to J. Chem. Phys. at the end of the week.
Many of the issues involved I have blogged about before. Here I will just mention two issues that I found particularly interesting. Both relate to the significance of very small changes in bond lengths due to quantum nuclear effects [tunneling and zero-point motion].
In hydrogen bonded complexes [A-H...B] one observes a subtle secondary isotope effect: when the hydrogen atom is replaced by a deuterium atom the distance R between the A and B atoms changes slightly, on the scale of one-hundredth of an Angstrom [and denoted Delta R]. Furthermore, as shown below, the variation of Delta R with R is a non-trivial non-monotonic function.
In the paper we show that for R less than 2.7 A these trends are captured semi-quantitatively by a very simple calculation which assumes that the effect is dominated by the variation with R of the zero-point energy of the A-H stretch.
This leads to the second result that I found both surprising and impressive. When R ~ 2.5 A, the D for H isotope substitution increases R to about 2.54 A. This apparently small change has another secondary effect: it produces a significant change in the energy barrier in the potential energy curve for the A-D stretch, compared to the A-H stretch. This in turn significantly changes the A-D stretch vibrational frequency. Indeed the A-H and A-D stretch can have similar frequencies, whereas for isolated molecules the frequency ratio would be close to 1.4=sqrt(2). This explains rather complicated and large isotope effects I blogged about more than two years ago.
Labels:
hydrogen bonds,
quantum chemistry,
tunneling
Saturday, January 18, 2014
Uncertainty about Heisenberg's motivation
It is very rare that physics is the centre of a play, particularly anything that receives popular or critical acclaim. An exception is the play, Copenhagen by Michael Frayn. It centres around the famous meeting between Heisenberg and Bohr, in Nazi-occupied Copenhagen in 1941.
I enjoyed watching the film version produced by the BBC. Daniel Craig [of James Bond fame] plays Werner Heisenberg. It nicely captures the complexities of not just Heisenberg's visit, but also that of the relationship between Heisenberg and his mentor, the role of Bohr's wife, the passion for physics, and the moral issues associated with nuclear weapons.
I enjoyed watching the film version produced by the BBC. Daniel Craig [of James Bond fame] plays Werner Heisenberg. It nicely captures the complexities of not just Heisenberg's visit, but also that of the relationship between Heisenberg and his mentor, the role of Bohr's wife, the passion for physics, and the moral issues associated with nuclear weapons.
Labels:
history,
movies,
nuclear physics,
politics,
quantum foundations
Thursday, January 16, 2014
Experiencing the heat of solution
It is always fascinating to me when one can experience some scientific concept in everyday life. I particularly like it when one can see things with the naked eye. Recently I realised that a macroscopic manifestation of spin-orbit coupling is ferromagnetic domains and hysteresis. This is because they arise from spin anisotropy which is due to spin-orbit coupling. But I digress.
The other day I was maintaining my pool [a bain of my existence] and I mixed some solid "Hardness increaser" in water. It got really warm! I had noticed this before but not thought about it much. Why does this happen? The chemical is mostly Calcium chloride. It turns out that this has a particularly large "heat of solution" [the enthalpy change associated with dissolving it in water] of -83 kJ/mol. For this reason it is used in "hot packs" and some undergraduate chemistry labs to illustrate heat of solution. [See articles one and two in the Journal of Chemical Education]. In thermal isolation dissolving 100 grams in 1 liter of water should raise the water by 18 degrees C. This is why I experienced it directly.
I am embarrassed that much of the chemistry involved in swimming pool maintenance remains a mystery to me. [e.g. What is the point of increasing the alkalinity and decreasing the pH at the same time?] But hopefully once I read this J. Chem. Ed. paper it will all become crystal clear.
The other day I was maintaining my pool [a bain of my existence] and I mixed some solid "Hardness increaser" in water. It got really warm! I had noticed this before but not thought about it much. Why does this happen? The chemical is mostly Calcium chloride. It turns out that this has a particularly large "heat of solution" [the enthalpy change associated with dissolving it in water] of -83 kJ/mol. For this reason it is used in "hot packs" and some undergraduate chemistry labs to illustrate heat of solution. [See articles one and two in the Journal of Chemical Education]. In thermal isolation dissolving 100 grams in 1 liter of water should raise the water by 18 degrees C. This is why I experienced it directly.
I am embarrassed that much of the chemistry involved in swimming pool maintenance remains a mystery to me. [e.g. What is the point of increasing the alkalinity and decreasing the pH at the same time?] But hopefully once I read this J. Chem. Ed. paper it will all become crystal clear.
Monday, January 13, 2014
Learning to live with limited affirmation
My apologies to readers who saw the draft beginnings of this post. I mistakenly posted it rather than saving it as a draft. Quite embarrassing.
Teenagers who don't receive enough affirmation at home will be prone to seek affirmation in the wrong places. (A classic and controversial issue is the possible correlation between absent fathers and teenage pregnancy).
Scientists are human and we all need and enjoy affirmation for our work. But, many of us don't get as much as we would like. Just like teenagers we are prone to seek affirmation from the wrong sources. We write papers that get rejected by luxury journals. We publish papers and they may be largely ignored. Our grant applications get rejected. We don't get the invited conference invitations that we think we deserve. This can be particularly hard for the young and inexperienced.
I think it is important to be secure in yourself about the quality of your work and not start seeking affirmation from the "wrong" crowd: luxury journals, funding agencies, pretentious older colleagues, administrative bean counters, .... Just like for teenagers it will end in tears...
An old post, The alternative to doing significant research discusses how in the classic C.P. Snow novel, The Masters, many of the characters have such a pitiful academic existence.
The Physics history column in the American Physical Society News recently featured a fascinating story, Perelman posts proof of the Poincare conjecture on the arXiv.
Perelman is clearly a very secure individual who only needed the satisfaction of doing good science.
Teenagers who don't receive enough affirmation at home will be prone to seek affirmation in the wrong places. (A classic and controversial issue is the possible correlation between absent fathers and teenage pregnancy).
Scientists are human and we all need and enjoy affirmation for our work. But, many of us don't get as much as we would like. Just like teenagers we are prone to seek affirmation from the wrong sources. We write papers that get rejected by luxury journals. We publish papers and they may be largely ignored. Our grant applications get rejected. We don't get the invited conference invitations that we think we deserve. This can be particularly hard for the young and inexperienced.
I think it is important to be secure in yourself about the quality of your work and not start seeking affirmation from the "wrong" crowd: luxury journals, funding agencies, pretentious older colleagues, administrative bean counters, .... Just like for teenagers it will end in tears...
An old post, The alternative to doing significant research discusses how in the classic C.P. Snow novel, The Masters, many of the characters have such a pitiful academic existence.
The Physics history column in the American Physical Society News recently featured a fascinating story, Perelman posts proof of the Poincare conjecture on the arXiv.
Perelman is clearly a very secure individual who only needed the satisfaction of doing good science.
Labels:
C.P. Snow,
job advice,
mathematics,
mental health
Wednesday, January 8, 2014
A basic but important research skill: initiative
Some basic research skills that I feel are important may be increasingly neglected in the training of students. I fear this neglect is partly due to the pressure to "produce" leading to people cutting corners and supervisors treating students like technicians.
The first skill is Take initiative.
Students, regardless of their limited knowledge and experience, should not sit around waiting for directions and feedback. They should not just do what they are told.
They should just "try stuff". What does this mean?
To begin with most of what you try may not work or will produce little of new interest.
But, you will slowly learn what works and what does not. Your intuition will increase. But you may get lucky and find something completely new.
Other basic skills include:
The first skill is Take initiative.
Students, regardless of their limited knowledge and experience, should not sit around waiting for directions and feedback. They should not just do what they are told.
They should just "try stuff". What does this mean?
- Look at the literature on your own, beyond what has been recommended to you.
- Try to reproduce other peoples results.
- Try doing the experiment under slightly different conditions. Try a different sample or device.
- Try doing the computer simulation with slightly different parameters.
- Try doing the analytical calculation using a different method.
- Ask questions.
To begin with most of what you try may not work or will produce little of new interest.
But, you will slowly learn what works and what does not. Your intuition will increase. But you may get lucky and find something completely new.
Other basic skills include:
- knowing the literature
- double checking results
- making comparisons
- getting feedback from others
- listening to referees
Monday, January 6, 2014
How many unique identities do I need?
I would appreciate some clarity and comments on the issue of "Researcher ID's".
A couple of years ago I made the mistake of signing up for "ResearchGate". This led to an incredible amount of spam in my email inbox.
Then my School was being reviewed and so all the staff had to sign up for "ResearcherID". This was quite some work because one had to "tag" all of your publications. Then I thought I was done...
Now I find that journals I publish in are asking for my ORCID.
I am reluctant to waste more time jumping through more hoops to create another "unique" identity.
But maybe this is the "special one", the author version of the DOI.
I am also getting tired/concerned/frustrated with all the metric focus.
I am also concerned how these initiatives seem to have a strong commercial element to them.
But, perhaps I just have to bite the bullet and do it.
I welcome comments and clarification.
A couple of years ago I made the mistake of signing up for "ResearchGate". This led to an incredible amount of spam in my email inbox.
Then my School was being reviewed and so all the staff had to sign up for "ResearcherID". This was quite some work because one had to "tag" all of your publications. Then I thought I was done...
Now I find that journals I publish in are asking for my ORCID.
I am reluctant to waste more time jumping through more hoops to create another "unique" identity.
But maybe this is the "special one", the author version of the DOI.
I am also getting tired/concerned/frustrated with all the metric focus.
I am also concerned how these initiatives seem to have a strong commercial element to them.
But, perhaps I just have to bite the bullet and do it.
I welcome comments and clarification.
Thursday, January 2, 2014
The challenge of improving education in the developing world
This video discusses the results contained in the Science article
The Challenge of Education and Learning in the Developing World
Michael Kremer, Conner Brannen, Rachel Glennerster
It uses the same approach of randomised trials that feature in the book Poor Economics.
Labels:
economics,
funding,
high school,
Majority world,
politics,
teaching
Subscribe to:
Posts (Atom)